The singularity of technology lies perhaps in its an aura of objectivity and timelessness whereas reality demonstrates just the opposite. Like everything else, it complies with the dictates of history and obeys conventions. André Gunthert goes back over some of the arguments that might bid us to rejoin the land of history, the land formalism’s supporters had left behind. Using some well-known examples to which we had never truly paid attention from the standpoint of technology, he reminds us that every recording operation–perceived as transparent at the moment it is carried out–has a tendency to become opaque as it recedes in time. In fact, there is no end to the redefinition of technology, as there is no end to the variations in taste, by nature temporary, that depend on this constant redefinition. Nothing takes place without a minimum of historical consensus, the most lasting of which indeed assures all possible aspects of immediacy and transparency.
Christian Walter extends to the economy this reflection on the pseudo neutrality of technology. What he shows us is that a market is dependent on its recording. The recent stock-market crisis would indeed have confirmed him in his insistence on the nature of the apprehension of uncertainty in the economic and financial worlds, where probabilistic modelings dating from the 1960s rest on statistical conceptions that are themselves inherited from the nineteenth century. According to Walter, the practices that follow therefrom are unsuited to take into consideration some of today’s major phenomena: spasms of opinion and liquidity crises. Arguing for a “clear image” of uncertainty, he sheds light on the role representation plays in economics as well as elsewhere.
Each in his own way and on the basis of very different objects of study, both authors demonstrate how powerful is the role technology plays. Deceptively innocent, technology succeeds insofar as the viewer does not desire to know what lurks behind its filters.
Laurence Bertrand Dorléac
Seminar of December 13th 2007
One of the characteristic features of contemporary finance is its massive mathematization. The objective of mathematical market models is to put the arrows on stock-market charts into equations, thereby socially building up a world of permanent exchange in which calculations of the value of things become a foundational convention in such exchanges. Stock-option prices, stock prices, but also prices for electricity or prices for tomorrow’s weather in Paris or in New York–nothing escapes the mathematical reach of contemporary finance. And conversely, this massive financialization of the world rests ultimately on the shared acceptance of powerful mathematical models performatively applied in financial actors’ computer systems, but also and especially, cognitively built into their ways of thinking reality. It is quite remarkable to observe how deeply this cognitive embedding extends among those very people who most express their distrust of models and who make a strong point of saying that they are exempt from them, such as professionals of so-called classical asset management. The main objective of such models is to quantify uncertainty and to transform it into a probability distribution. The image of uncertainty stock-exchange movements give thus becomes the underpinning for the calibration of the risk of market positions. In their concrete practices, professionals implement this calibration of probabilities on a very deep level–even down to that of the very organigrams of banking institutions and asset-management firms. International regulations then come to solidify into restrictive professional norms the conception of uncertainty that stemmed from probabilistic modelings of stock-market fluctuations.
In view of the depth of this penetration on the intellectual level, it may be interesting, nay socially useful, to investigate the conceptual bases of such probabilistic models. Indeed, this putting of risk into equations (like the calculation of value) is in fact the result of a completely nontrivial intellectual operation that involves a twofold reconstruction of the financial world. There is, first of all, an empirical reconstruction and then a theoretical one. The empirical reconstruction, which involves the image of the market that shows up on charts representing stock-market fluctuations, depends on how one takes in stock-quote data, and therefore on the technologies for recording such data. In the theoretical reconstruction that takes place, the choices of mathematical models are based on the image produced by these recordings, which then serve to validate statistically the probabilistic choices implemented in these models. At the end of this process of a twofold reconstruction of the world, it could be said that the real market has been replaced by the image thereof, which is supposed to represent it adequately; but more precisely, it would be fairer to say that one has socially constructed a financial world that rests on the perception of an image of its fluctuations. Let us now see more closely what this is all about.
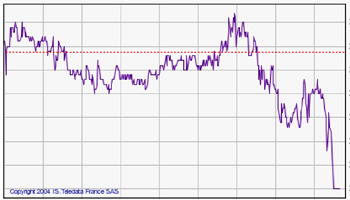
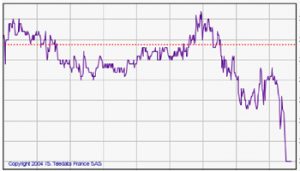
Fig. 1 Stock-market fluctuations on the microscopic scale of transactions.
The basic component of the recording is the quotation of a security at the moment of its exchange. This quotation is noted down with each exchange, and in this way one constructs a series of prices that, connected together, plots out a stock-market arrow, the one showing the traded security’s evolution over time (Figure 1). The clock (or calendar) measuring the fluctuations is constituted here by the succession of quotation-dates: this is, therefore, a time that is intrinsic to the market–“exchange time” and not “physical” calendar time. On the basis of such databases, one can then construct a new series of data via a simple process of aggregation: by adding the successive price variations exchange by exchange, one obtains the successive price variations every second exchange, then every third, and so on, until one obtains chronological series of daily, weekly, monthly, and then annual price variations (Figure 2). This new series is constructed along a timeline that is no longer based on intrinsic time but on physical time, or “everyone’s time,” as opposed to the preceding time which would be, rather, the “time of a few.”
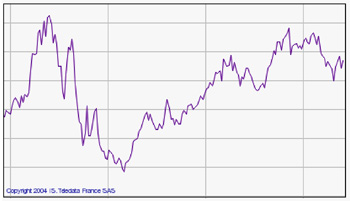
Fig. 2 Stock-market fluctuations on the macroscopic scale of economies.
The databases (built up quotation by quotation) are high-frequency–or, high-resolution–market-image data, whereas aggregated (for example, annual) data are low-frequency, or low-resolution, market-image data. To understand well the import of such high-frequency data, we need to be able to design a very specific market microstructure theory (who holds what in portfolio; how order books are cleared, etc.). We find ourselves here on the microscopic scale of price formation in the reduced social space of the market. On the other hand, low-frequency databases allow more comparisons of stock-market variations to variations in classical economic figures (GNP, etc.): here we find ourselves on the macroscopic scale of States and economic policies, in another social space. Is there a “right” scale for the observation of markets, a correct distance from the stock-market arrow’s image? When one looks at a picture or a photograph, observational distance becomes an important element in one’s appreciation of the representation. Should one be closer to or further from the stock-market arrow (Figure 3)? Should one seek to scrutinize the details of the stock-market painting, or can one just make do with a view of its overall forms?
Let us pursue this analogy with photography. In low resolution, images appear blurry when they are enlarged (or “pixilated”). Low resolution represents a loss of information about the object photographed. What about the market? Does one lose information when one passes from high-frequency data to low-frequency data? The answer is provided by Mandelbrot’s theory of fractals: if stock-market variations are fractal, the choice of resolution-scale has no impact on one’s obtainment of information. There is scale invariance, and the structure of the details does not disappear when one changes one’s distance from the image. A fractal preserves the same details on all scales. In the opposite case, the change in resolution necessarily induces a change in the image of uncertainty and therefore a change in access to the information. It is apparent that images of uncertainty that stem from the statistical treatment of high-frequency data did not correspond to those stemming from the statistical treatment of low-frequency data. Fractal theory does not apply uniformly or in a direct manner to price variations.
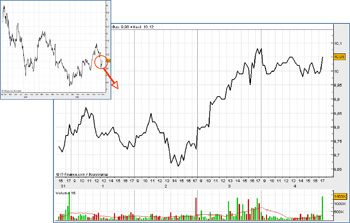
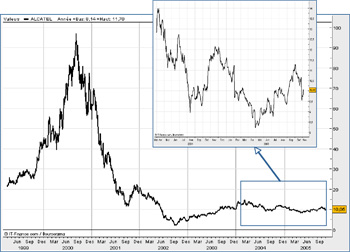
Fig. 3 Changes of scale and zoom shots depending on the recording technology in use for Alcatel stock: (a) From 7 years to 2 years; (b) from 2 years to 4 days.
Recording technologies have varied over the course of time with the development of electronics and of computing power. In the 1930s, the data were compiled quarterly. They became daily in the 1970s, then intraday in the 1990s. Now, at the moment the data are recorded, the technology itself is invisible and transparent: the state of the technological apparatus therefore disappears when constructing probabilistic models. But subsequent obsolescence makes it apparent. From one era of recording to the next, one does not see the market in the same way, or not the same market. Thus, new technologies have led to a substantial modification in the understanding of stock-market variations and therefore, as we have understood, in the image of uncertainty affecting market movements. New probabilistic models appeared in the 1990s that represented more faithfully what one was seeing and what one was not seeing previously, and this new vision of the markets has led to a new conceptualization of risk.
And yet in professional financial circles, what one has observed is resistance to this change in conceptualization–with, on the one hand, a preservation of probabilistic models unsuited to the new image of uncertainty and, on the other hand and in a more insidious way, maintenance of cognitive embeddedness in the old conception of risk that stemmed from 1960s technology. The financial crises we have known recently come, in part, from this gap between the updated image of uncertainty we now have and the maintenance of probabilistic modelings that stem from an older image (and therefore from an older recording technology). We may ask: Is there a conflict of recording technologies, or is something else involved here? Does one see nothing, or does one want to see nothing?
This question leads us to rethink the notion of time and therefore of the suitable speed for viewing the film of the market. Like fast motion or slow motion in film, exchange time seems to dilate or contract along with stock-market activity. Financial risk depends on these temporal pulsations, and the successful navigation by the best portfolio managers (such as Warren Buffet) upon these chronological waves shows that they know how to use social time (or kairos) and not physical time (chronos) as their reference point. For them, a week in the stock market week can last less than one turbulent morning. Might exchange time be irreducible to calendar time? On markets, it would seem that, as the Psalmist said, a day is as a thousand years, and a thousand years are as one day (II Peter 3:8).
Bibliographie
Lévy, Véhel J. and Christian Walter. Les marchés fractals. Paris: Presses Universitaires de France, 2002.
Walter, Christian, and Éric Brian. Eds. Critique de la valeur fondamentale. Paris: Springer, 2007.
Christian Walter, a graduate of the École supérieure des sciences économiques et commerciales who holds the Institute of Actuaries of France (IAF)’s actuarial agrégation, has a doctorate in economics, and is authorized to supervise student dissertations, is an associate professor at Sciences Po and a consultant. His work deals with financial modeling as well as the history and epistemology of financial theory. Walter has twenty years of professional experience in managing assets and controlling risk (CCF, BBL, SBS, Crédit Lyonnais, Pricewaterhouse Coopers). He is also a member of the Scientific Council of the French Association of Financial Management (AFG).
